Espacio Muestral (S) : Todas las salidas probables de un experiemento.
Ejemplos:
a) Lanzar una moneda: S = {Cara, Cruz}
b) Medida de Distancia: S = { |R+ } (el conjunto de números reales positivos)
Variable Aleatoria: Es una función que asigna un numero real a cada elemento de S. Se las denota con letra mayúscula para distinguirlas de su valor que también puede ser una variable pero escrita en minúscula.
Ejemplos:
a) Lanzar una moneda: Cara=0, Cruz=1
b) Medida de Distancia: X = x
La suma de probabilidades de todos los valores de la variable aleatoria es 1.
Es conveniente en los casos de variable continua representar p(X=x) como fx(x) llamada función de densidad de probabilidad.
Valor Esperado: Es el valor de una variable aleatoria que esperamos obtener mayor cantidad de veces al realizar varias veces el mismo experimento. Sin embargo a veces es un valor imposible. (Imposible: Probabilidad de que X = x es cero, p(X = x) = 0 )
En muchos caso es más fácil considerar la esperanza como:
Varianza: Es un valor que indica que tan dispersa es X con respecto a su valor esperado. Se representa como o Var(X) =
o Var(X) =
Valor Esperado: Es el valor de una variable aleatoria que esperamos obtener mayor cantidad de veces al realizar varias veces el mismo experimento. Sin embargo a veces es un valor imposible. (Imposible: Probabilidad de que X = x es cero, p(X = x) = 0 )
En muchos caso es más fácil considerar la esperanza como:
Varianza: Es un valor que indica que tan dispersa es X con respecto a su valor esperado. Se representa como
 o Var(X) =
o Var(X) =
Distribución Conjunta: Es la probabilidad de que los eventos X=x y Y=y sucedan al mismo tiempo.
Probabilidad Condicional: Es la probabilidad de que suceda X=x dado que esta sucediendo o ya sucedió Y=y.
En el ejemplo del partido de fútbol la probabilidad de X=ganar dado que Y=perder es 1, ya que no puede darse X=perder si se dan los otros dos casos de Y.
Probabilidad Total : De lo anterior se tiene:
Marginales: Es la obtención de fx(x) y fy(y) a partir de fx,y(x,y).
Por ejemplo en un partido de fútbol, que tiene tres posibles salidas para X y Y que representan el resultado para cada equipo (perder, empatar o ganar), P(X=x, Y=y) tiene valor de 0 para X=ganar y Y=ganar y también para X=perder y Y=perder, dado que no se pueden dar ambos al mismo tiempo.
Probabilidad Condicional: Es la probabilidad de que suceda X=x dado que esta sucediendo o ya sucedió Y=y.
En el ejemplo del partido de fútbol la probabilidad de X=ganar dado que Y=perder es 1, ya que no puede darse X=perder si se dan los otros dos casos de Y.
Probabilidad Total : De lo anterior se tiene:
Si se suma con respecto a todos los valores de Y obtendríamos la probabilidad de obtener X, o sea fx(x).
Marginales: Es la obtención de fx(x) y fy(y) a partir de fx,y(x,y).
Teorema de Bayes: En las ecuaciones de obtención de marginales se observa una relación interesante y es que la distribución conjunta es igual a X dado Y por la probabilidad de Y y a la vez es la probabilidad de Y dado X por la probabilidad de X. Uniendo estas dos relaciones resulta que se puede conocer cualquier probabilidad entre dos variables si se conoce al menos una probabilidad condicional y la de una variable
Independencia: X y Y son independientes si:
Por ejemplo si X es el resultado de lanzar una moneda y Y el de lanzar otra, los resultados no dependen entre si, incluso Y puede ser un segundo lanzamiento de la misma moneda.
Si existe una tercera variable aleatoria Z, X y Y son condicionalmente independientes si:
Por último en este recuento la distribución de probabilidad más usada, llamada gaussiana o normal. Su función de densidad es:
Y un ejemplo:
Suponga hay dos variables aleatorias Puerta (abierta, cerrada) y Luz (prendida, apagada), se busca p(Puerta|Luz) que es un razonamiento de diagnóstico a cambio de p(Luz|Puerta) que es un razonamiento de causal. A menudo el conocimiento causal es mas fácil de obtener, mediante Bayes podemos dejar p(Puerta|Luz) en términos de conocimiento causal.
Como conclusión se nota que el conocer que la luz está prendida da mayor probabilidad que la puerta este abierta.
Al final este artículo es un resumen de la teoría matemática de probabilidad.
En el próximo artículo continuaremos el análisis de este ejemplo para derivar el filtro de Bayes y una breve explicación de las Cadenas de Markov.








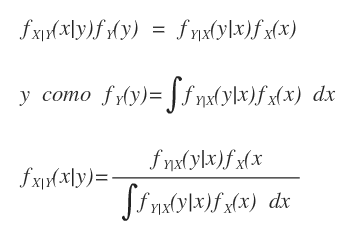






No hay comentarios:
Publicar un comentario