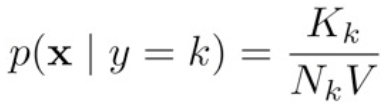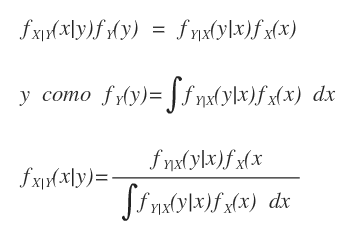ML IV: Regresión o Ajuste

Diferencias entre Regresión y Clasificación:

• En la regresión, Y, la variable dada a las clases, es continua, en la clasificación es discreta 

• La regresión aprende una función, la clasificación normalmente aprende etiquetas de clase. 

Por ahora vamos a tratar de regresión.

Funciones de Base: 

En principio, los elementos de X pueden ser cualquier cosa (por ejemplo, números reales, gráficos, objetos 3D). Para poder tratar estos objetos matemáticamente necesitamos funciones que asignen un número real a partir de X. Llamamos a estas las funciones de base. 

También podemos interpretar las funciones de base como las funciones que extraen las características de los datos de entrada. Estas características reflejan las propiedades de los objetos (anchura, altura, etc.)

El problema de regresión lineal puede ser planteado como sigue:

Asumir que X pertenece a los números Reales, Y pertenece a los números Reales también, la función Ø es la identidad (I)

Dados: Puntos de datos (x1,t1); (x2,t2), ...

Objetivo: Predecir el  valor de t para una nueva muestra de x.

Formulación Paramétrica: y(x,w)=w0+w1x

Para llegar al objetivo podemos usar el error cometido (líneas verdes) entre el valor predicho al evaluar la función (línea negra) y el valor de un punto dado(puntos rojos). 

Si usamos la suma de todos esos errores sin importar el signo (puesto que hay puntos arriba y abajo de la línea) basta con conocer cuales w0 y w1 minimizan dicho error, logrando que el valor predicho tenga poco error 

A la siguiente función de error se le llama suma de error cuadrático medio:

Como el error es elevado al cuadrado y se busca minimizarlo a este método se le conoce como mínimos cuadrados. La manera en que se halla el mínimo de una función es derivándola, como w =[w0 w1] es decir no es una variable única si no varias se utiliza el operador de gradiente (triángulo invertido) que deriva la función para cada variable quedando de resultado otro vector.

Con estas dos ecuaciones es posible llegar al resultado, veamos con un programa en Scilab, usando la formula resultante:

Primero daremos puntos cercanos a una recta conocida, luego calcularemos w aplicando la función linsolve(A,b) que resuelve el problema de álgebra lineal Ax+b=0. Pondremos todo dentro de una función reglineal(x,t), que recibe como datos los puntos y devuelve w y la gráfica de los puntos y la recta encontrada.

En un archivo nuevo en SciNotes copia y guarda como reglineal.sci

//Función que realiza la regresión lineal de los puntos dados

//x: es un arreglo(vector) unidimensional correspondiente a la variable x.             Arreglo(float)

//t: es un arreglo(vector) unidimensional correspondiente a la variable t.             Arreglo(float)

//w: Son los coeficiente de la funci[on lineal. Arreglo(float)

function w = reglineal(x, t )

  xi=[ones(1,length(x));x];

  A=(xi*xi')'//la comilla simple significa transponer o el superindice T de las ecuaciones

  b=(t*xi')';

  w=linsolve(A,-b);//Es -b pues tiene que volver del otro lado del igual

  y=w'*xi;

  figure();

  plot(x,t,'or'); //La 'o' hace que se dibujen solo los puntos, la 'r' que sean rojos.

  plot(x,y,'k'); //la 'k' hace negra la linea.

endfunction     

En otro archivo o copiando directamente en la interfaz de comandos pon:

clc

x=[0 1 2 3 4 5 6 7 8 9];

t=[3 8 13 18 23 28 33 38 43 48];

w=reglineal(x,t);

disp(w, "Los coeficientes w resultaron");

//El resultado debe ser [3 5], es decir y=3+5*x.

////Ahora observemos que pasa al ingresar las varibles en otro orden

//Se espera  la misma expresion despejando x=-3/5+1/5*y= -0.6+0.2y

w1=reglineal(t,x);

disp(w1, "Los coeficientes al invertir las variables son ");

//por ultimo ingresemos valores no exactos para ver a que se aproxima

xh=[0 1 2 3 4 5 6 7 8 9];

th=[4 6.5 11.7 16 25 28.5 32 37.8 44 48.1];

w2=reglineal(xh,th);

disp(w2, "Los coeficientes ahora son son ");

w3=reglineal(th,xh);

disp(w3, "Los coeficientes al invertir las nuevas varibles son ");

//Ahora observemos como no necesariamente se llega al mismo resultado al ingresar las variables en otro orden

 //Se espera x=-0.473140+0.1961017y 

El problema de regresión polinómica se plantea como sigue:

Asumir que X pertenece a los números Reales, Y pertenece a los números Reales también, la función Øj es x elevado a la j.

Dados: Puntos de datos (x1,t1); (x2,t2), ..., (xN,tN)

Objetivo: Predecir el  valor de t para una nueva muestra de x.

 La función paramétrica se muestra en la figura, donde M es la complejidad dado que indica el  número de coeficientes de y.

Al poner y(x,w) con notación vectorial, considerando Ø(x) también como un vector:

Al igual que en el caso anterior se debe minimizar E(w), pero ahora no son solo dos variables sino N variables.

Al final queda:

Con:

Realizemos el siguiente ejercicio en Scilab:

Copia la siguiente función y guarda como regpolinomial.sci

//Función que realiza la regresión polinomial de los puntos dados

//x: es un arreglo(vector) unidimensional correspondiente a la variable x.             Arreglo(float)

//t: es un arreglo(vector) unidimensional correspondiente a la variable t.             Arreglo(float)

//m: es la complejidad del polinomio, m-1 es el grado 

//w: Son los coeficientes del polinomio. Arreglo(float)

function w = regpolinomial(x, t ,m)

    for i=1:length(x)

        for j=1:m

            phi(i,j)= x(i)^(j-1);

        end

    end

  A=phi'*phi

  b=phi'*t';

  w=linsolve(A,-b);//Es -b pues tiene que volver del otro lado del igual

  y=w'*phi';

  figure();

  plot(x,t,'or'); //La 'o' hace que se dibujen solo los puntos, la 'r' que sean rojos.

  plot(x,y,'k'); //la 'k' hace negra la linea.

endfunction    

Copia el siguiente código en un archivo o directamente en la interfaz de comandos:

clc

//Datos aleatorios

x=[0 1 2 3 4 5 6 7 8 9];

t=[2 13 20 53 78 83 98 103 128 125];

m=4;

w=regpolinomial(x,t,m);

disp(w, "Los coeficientes w con m=3 resultaron ");

w1=regpolinomial(t,x,m);

disp(w1, "Los coeficientes w al invertir el orden de entrada de los puntos esultaron");

m=32; 

w2=regpolinomial(x,t,m);

disp(w2, "Los coeficientes w con m=32 resultaron");

w3=regpolinomial(t,x,m);

disp(w3, "Los coeficientes w con m=32 al invertir el orden de entrada de los puntos resultaron");

En las diapositivas también encontramos este ejemplo:

En las primeras 4 gráficas se observa los resultados al aumentar la complejidad, al igual que en nuestro ejercicio en Scilab, es evidente que aumentar la complejidad no necesariamente ayuda a obtener un mejor ajuste, puede empeorar o producir sobreajuste (N=10, M=10), por el contrario en las 4 gráficas siguientes se observa como el añadir puntos de datos si mejora el ajuste obtenido. 

Se puede usar otras funciones base, como la gaussiana 

 Y la sigmoidal:

Como se aprecia en todas las figuras la complejidad de la regresión debe llegar a ser la adecuada par obtener un buen resultado y debido a que el número de datos disponibles generalmente es fijo se debe hallar cual debe ser ese nivel de complejidad .  

ML III: Aprendizaje

Un robot para poder interactuar con su entorno tiene que conocer que es lo que hay en su entrono. Para esto debe clasificar los objetos tomando sus características físicas o funcionales como parámetros de entrada.
Una manera natural de clasificar objetos es aprender las categorías a las que pueden pertenecer y después colocarlos dentro de una de ellas. La idea del Machine Learning es hacer este aprendizaje automático.
Partiendo de las ideas anteriores, supongamos un conjunto X de objetos y un conjunto Y de categorías, ahora buscamos que todos los elementos similares de X sean asignados a un Y.

Asignación a una categoría 

Puede considerarse categorías muy generales como en el ejemplo de la imagen de arriba, o categorías tan específicas como la raza a la cual pertenece el gato. Esto depende de la aplicación y utilidad que vamos a dar al uso de inteligencia artificial. El siguiente cuadro muestra las formas de realizar el aprendizaje.

En los siguinetes artículos se va a usar principalmente el aprendizaje supervisado y empezaremos con un ejemplo de Modelo Generativo, cuyo enunciado es el siguiente:

Clasificación más cercana al vecino:
• Dado: Puntos de Datos (x1,y1); (x2,y2)
• Regla: Cada nuevo elemento de datos se asigna a la clase de su vecino más cercano en el espacio de características.
Gráficamente este problema se resuelve como sigue:

Ahora podemos realizar un analisis para el caso general de K vecinos cercanos, denominando Kk como los puntos que pertenecen a la clase k dentro de una esfera con volumen V y Nk a todos los puntos de la clase k. Además K son todos los puntos dentro de la esfera y N el total de puntos. Con  esto hallamos:

Y usando Bayes finalmente:

Para clasificar un nuevo punto basta con sacar p(y=k| x) para toda k y escoger la clase que nos devuelva el máximo valor, esto quiere decir tomar la clase para la cual existen más vecinos cercanos de esa misma clase.

ML II: Asunción de Markov y Redes Bayesianas.

Siguiendo con el ejemplo del artículo anterior que pasa si agregamos una nueva medida del sensor de luz, representada por la variable aleatoria Luz2. Queremos ahora conocer p(Puerta=abierta|Luz1, Luz2).
Usando Bayes tenemos:

Ahora sabemos que Luz1 no afecta a la medida de Luz2, por tanto son variables independientes y condicionalmente independientes dado Puerta.

Esto es llamado la Asunción de Markov, pues no depende del estado anterior.

Realizando el cálculo al reemplazar valores resulta:

P: Puerta, L1: Luz1, L2: Luz2
Con datos:

Como conclusión se nota que el conocer Luz2 merma la probabilidad de que la puerta este abierta en comparación a cuando solo se conocía Luz1.

Asunción de Markov. Más formalmente se define, asumiendo que se tienen medidas Zn condicionalmente independientes a otra variable X.

Ahora llevemos el ejemplo a  Sensar y Actuar, es decir el robot conoce si la puerta esta abierta o cerrada y actúa en consecuencia cerrándola o abriéndola. (Un sencillo Agente Inteligente)

Para esto modelemos la acción como una variable aleatoria U=u, y queremos conocer la probabilidad condicional de p(Puerta|U). 

 El gráfico de arriba muestra las probabilidades de transición de pasar de la puerta abierta a cerrada, un 90%, viceversa o que se mantenga en el mismo estado.

Donde P: Puerta, PA: Puerta en su estado anterior, U: acción. Y con los datos del último ejemplo se tiene

Al final interesa la p(Puerta=cerrada|u) por que con el sensor tratábamos de conocer si la puerta está abierta  y el objetivo es cerrar la puerta.

Por eso hasta ahora logramos conseguir el estado del sistema mediante la actualización por el sensor y por la acción realizada. Ahora tratemos de combinar ambas.

Para eso definiremos la creencia (Belief). 

Podemos describir el proceso general mediante una Red Bayesiana Dinámica:

Esto incorpora las siguientes Asunciones de Markov:

Con estas ultimas expresiones usando Bayes se llega a:

Dado que la creencia es recursiva es posible realizar su calculo mediante un algoritmo:

 Algoritmo Filtro de Bayes (Bel(x),d)

 El filtro de Bayes es principalmente usado en: 

• Filtro de Kalman.
• Filtro de Partículas.
• Modelos Ocultos de Markov
• Redes  Bayesianas Dinámicas.
• Procesos de Decisión de Markov Parcialmente Observables.

Que a su vez son usados en clasificación de patrones y seguimiento de objetos en imágenes.

En resumen:

• El razonamiento probabilístico es necesaria para hacer frente a la información incierta, por ejemplo, mediciones de sensores 

• Usando la regla de Bayes, podemos hacer el razonamiento de diagnóstico basados en el conocimiento causal 

• El resultado de las acciones de un robot se puede describir mediante un diagrama de transición de estado. 

• La estimación de estado probabilístico se puede hacer de forma recursiva mediante el filtro de Bayes usando un sensor y una actualización de movimiento 

• Una representación gráfica para el problema de estimación de estado es la Red Bayesiana Dinámica.

Scilab

Ahora como ejercicio en Scilab crearemos una función Normal de probabilidad e implementaremos una integral. Para la integral usaremos simplemente su definición que es la de una suma de la función tomada en pequeños intervalos.

Primero abrimos Scilab y dentro de este a SciNotes.

En este editor escribiremos el siguiente código:

//Función de una densidad de probabilidad normal

//x: es un arreglo unidimensional del dominio de la función. Arreglo(float) 

//u: es el valor esperado o media. float

//s2: es la varianza de la densidad. float  

function fnormal = normal(x, u, s2 )

    fnormal=1/(sqrt(2*%pi*s2))*exp(-(x-u).^2/(2*s2));

endfunction    

Y guardamos como norma.sci. Ejecutamos con el símbolo de Play

Luego en un nuevo archivo copiamos el siguiente código:

//Función para calcular una integral definida

//x: es un arreglo(vector) unidimensional del dominio de la función

//fx: es la función. Arreglo(float)

//a: limite inferior de la integral. float

//b: limite superior de la integral. float

function F=integral(x,fx,a,b)

    delta=x(2)-x(1); //Separación en el eje x

    F=0; //Valor inicial

    j=1; //Variables auxiliares

    inf=1;

    sup=length(x);

//Primero comprobamos que los limites dados estén dentro del dominio

    if x(1)>a | x(1)>b then

        messagebox("Limite inferior erroneo, funcion no definida", "Error", "error");

    end

    if b>x(length(x))| a>x(length(x)) then

        messagebox("Limite superior erroneo, funcion no definida", "Error", "error");

    end

//Segundo encontramos los limites en nuestro arreglo x.

//sup indicara el indice del limite superior e inf el indice del limite inferior

    if b>a then

        while(x(j)<b & j<length(x))

            if x(j)<=a then

                inf=j;  

            end

        j=j+1;

        end

    sup=j;

//Calculamos la integral sumando los valore, como delta es constante se multiplica al final    

for i=inf:sup

        F=F+fx(i)

    end

    F=F*delta;

elseif b<a then

    while(x(j)<a & j<length(x))

        if x(j)<=b then

            inf=j;  

        end

        j=j+1;

    end

    sup=j;

    for i=inf+1:sup

       F=F-fx(i); 

    end

    F=F*delta;

    

    end

endfunction

//Función para obtener la función resultante de integra fx, 

//es la integral indefinida o pues no tiene limites definidos

//x: es un arreglo(vector) unidimensional del dominio de la función

//fx: es la función. Arreglo(float)

function IndF=fintegral(x,fx)

   delta=x(2)-x(1); 

IndF=zeros(length(x));

IndF(1)=fx(1)*delta;

//IndF ya no es un valor sino otro vector que tiene como datos los valores la integral

 for i=2:length(x)

        IndF(i)=IndF(i-1)+fx(i)*delta;

    end

return IndF

endfunction

Guarda como integral.sci y ejecuta.

Finalmente copia esto en la interfaz principal y presiona enter o crea un nuevo archivo y ejecuta

clc

//Dominio de las funciones

x=-30:0.01:30;

//Ejemplos de Densidades

pdf1=normal(x,0,1);

pdf2=normal(x,0,49);

pdf3=normal(x,4,1);

pdf4=normal(x,-10,9);

//Dibujar

plot(x,pdf1,'r-.',x,pdf2,'b--',x,pdf3,'g-',x,pdf4,'m:');

//r=rojo, b=azul, g=verde, m=magenta

//Probabilidad de que X de pdf1 este entre 0 y 1

Prob=integral(x,pdf1,0,1);

PDF=fintegral(x,normal(x,3,40));

figure();

plot(x,PDF);

disp(Prob, "La probabilidad de X es de ");

Si te salen estas figuras lo has hecho todo bien:

Con relación a la figura 2 se puede observar que PDF es una función creciente que empieza en su parte izquierda con 0 y en la parte más a la derecha tiene el valor de 1. A esto se le llama la función de distribución de probabilidad.

Como ultimo punto ingresa estas lineas  una por una en la interfaz principal, sin punto y coma para que se muestre el resultado

Prob1=integral(x,pdf1,-1,1)

Prob2=integral(x,pdf1,-2,2)

Prob3=integral(x,pdf1,-3,3)

Prob4=integral(x,pdf1,-4,4)

Prob5=integral(x,pdf1,-5,5)

Prob6=integral(x,pdf1,-6,6)

Estas son las probabilidades de la gaussiana normalizada, con media cero y varianza uno, para 1,2,3,4,5 y 6 varianzas o . Esto nos sirve para verificar nuestra integral ya que segun wikipedia los valores exactos de la llamada función error son:

Como punto adicional puedes ver cual es el error de nuestro método para integrar, pues existen otros métodos numéricos diseñados para realizar justamente este tipo de integrales que son casi imposibles de realizar manualmente.

ML I: Introducción a la Probabilidad.

Un recuento de probabilidad:

Espacio Muestral (S) : Todas las salidas probables de un experiemento.
Ejemplos:
a) Lanzar una moneda: S = {Cara, Cruz}
b) Medida de Distancia: S = { |R+ } (el conjunto de números reales positivos)

Variable Aleatoria: Es una función que asigna un numero real a cada elemento de S. Se las denota con letra mayúscula para distinguirlas de su valor que también puede ser una variable pero escrita en minúscula.
Ejemplos:
a) Lanzar una moneda: Cara=0, Cruz=1
b) Medida de Distancia: X = x
La suma de probabilidades de todos los valores de la variable aleatoria es 1.

Es conveniente en los casos de variable continua representar p(X=x) como fx(x) llamada función de densidad de probabilidad.  

Valor Esperado: Es el valor de una variable aleatoria que esperamos obtener mayor cantidad de veces al realizar varias veces el mismo experimento. Sin embargo a veces es un valor imposible. (Imposible: Probabilidad de que X = x es cero, p(X = x) = 0 )

En muchos caso es más fácil considerar la esperanza como:

Varianza: Es un valor que indica que tan dispersa es X con respecto a su valor esperado. Se representa como o  Var(X) =

Distribución Conjunta: Es la probabilidad de que los eventos X=x y  Y=y sucedan al mismo tiempo.

Por ejemplo en un partido de fútbol, que tiene tres posibles salidas para X y Y que representan el resultado para cada equipo (perder, empatar o ganar), P(X=x, Y=y) tiene valor de 0 para X=ganar y Y=ganar y también para X=perder y Y=perder, dado que no se pueden dar ambos al mismo tiempo.

Probabilidad Condicional: Es la probabilidad de que suceda X=x dado que esta sucediendo o ya sucedió Y=y.

En el ejemplo del partido de fútbol la probabilidad de X=ganar dado que Y=perder es 1, ya que no puede darse X=perder si se dan los otros dos casos de Y.

Probabilidad Total :  De lo anterior se tiene:

Si se suma con respecto a todos los valores de Y obtendríamos la probabilidad de obtener X, o sea  fx(x).

Marginales: Es la obtención de fx(x) y fy(y) a partir de fx,y(x,y).

Teorema de Bayes: En las ecuaciones de obtención de marginales se observa una relación interesante y es que la distribución conjunta es igual a X dado Y por la probabilidad de Y y a la vez es la probabilidad de Y dado X por la probabilidad de X. Uniendo estas dos relaciones resulta que se puede conocer cualquier probabilidad  entre dos variables si se conoce al menos una probabilidad condicional y la de una variable

Independencia: X y Y son independientes si: 

Por ejemplo si X es el resultado de lanzar una moneda y Y el de lanzar otra, los resultados no dependen entre si, incluso Y puede ser un segundo lanzamiento de la misma moneda.

Si existe una tercera variable aleatoria Z, X y Y son condicionalmente independientes si:

Por último en este recuento la distribución de probabilidad más usada, llamada gaussiana o normal. Su función de densidad es:

Y un ejemplo:

Suponga hay dos variables aleatorias Puerta (abierta, cerrada) y Luz (prendida, apagada), se busca p(Puerta|Luz) que es un razonamiento de diagnóstico a cambio de p(Luz|Puerta) que es un razonamiento de causal. A menudo el conocimiento causal es mas fácil de obtener, mediante Bayes podemos dejar  p(Puerta|Luz) en términos de conocimiento causal.

Como conclusión se nota que el conocer que la luz está prendida da mayor probabilidad que la puerta este abierta.

Al final este artículo es un resumen de la teoría matemática de probabilidad.

En el próximo artículo continuaremos el análisis de este ejemplo para derivar el filtro de Bayes y una breve explicación de las Cadenas de Markov.