REDES NEURONALES - BACK PROPAGATION PERCEPTRON CON UNA CAPA OCULTA

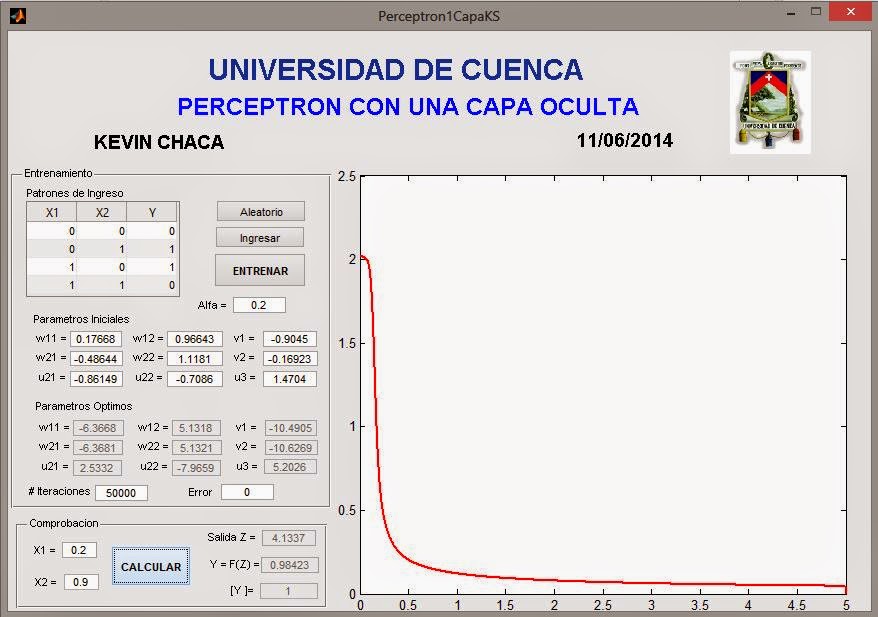
Una de las bases de la inteligencia artificial es la neurona artificial. Las capas ocultas en una red neuronal permite resolver problemas no linealmente separables. A continuacion se muestra el esquema, codigo y programa en MATLAB para resolver la compuerta logica XOR a traves del entrenamiento por el metodo de BACK PROPAGATION de una red neuronal con una capa oculta.

Esta red neuronal se compone de dos entradas, una capa oculta con 2 neuronas y una salida en la ultima capa. El esquema de la red neuronal se muestra en la siguiente figura:

El programa calcula los pesos del esquema utiiliando el metodo de Back Propagation con el metodo de aprendizaje delta.

PERCEPTRON CON UNA CAPA OCULTA Back Propagation XOR

%BOTON ENTRENAR.
function btEntrenar_Callback(hObject, eventdata, handles)
    %Obtener Datos de Tabla
    datos=get(handles.Tabla,'Data');
    x1=datos(:,1);
    x2=datos(:,2);
    yd=datos(:,3);

    %Otener datos iniciales de pesos y bias
    w110= str2double(get(handles.w110,'String'));
    w120= str2double(get(handles.w120,'String'));
    w210= str2double(get(handles.w210,'String'));
    w220= str2double(get(handles.w220,'String'));
    v10= str2double(get(handles.v10,'String'));
    v20= str2double(get(handles.v20,'String'));
    u210= str2double(get(handles.u210,'String'));
    u220= str2double(get(handles.u220,'String'));
    u30= str2double(get(handles.u30,'String'));
    alfa= str2double(get(handles.alfa,'String'));
 
    %Otener datos de iteraciones y error
    iteracionmax = str2double(get(handles.Iteraciones,'String'));
    errormax = str2double(get(handles.Error,'String'));

    %ENTRENAMIENTO
    w11= w110;
    w12=w120;
    w21= w210;
    w22= w220;
    v1= v10;
    v2= v20;
    u21= u210;
    u22= u220;
    u3= u30;
    condicion = 0;
    iteracion = 0;
    error_Total = zeros(1,iteracionmax+1);
    while(condicion == 0)
        for j = 1 : 4
            %Calcular la yObtenida
            %Capa Entrada
            z1 = x1(j);
            a11 = z1;
            z2 = x2(j);
            a12 = z2;

            %Capa Oculta
            z3 = a11*w11+a12*w21 + u21;
            a21 = funcion_activ(z3);
            z4 = a11*w12+a12*w22 + u22;
            a22 = funcion_activ(z4);

            %Capa Salida
            z5 = a21*v1 + a22*v2 + u3;
            yObtenida = funcion_activ(z5);

            %Calculamos error yObtenida*(1-yObtenida)*
            err = (yd(j)- yObtenida);

            %Correccion pesos Capa 2-3
            z= v1*a21+v2*a22+u3;
            d3 = err*derivada_fun_act(z);
            v1 = v1 + alfa*d3*a21;
            v2 = v2 + alfa*d3*a22;
            u3 = u3 + alfa*d3;

            %Correccion pesos Capa 1-2
            d21 = derivada_fun_act(z3)*v1*d3;
            w11 = w11 + alfa*d21*a11;
            w21 = w21 + alfa*d21*a12;
            u21 = u21 + alfa*d21;

            d22 = derivada_fun_act(z4)*v2*d3;
            w12 = w12 + alfa*d22*a11;
            w22 = w22 + alfa*d22*a12;
            u22 = u22 + alfa*d22;

            %Contar error total
            error_Total(iteracion+1) = error_Total(iteracion+1)+abs(err);
        end
        iteracion = iteracion +1
        if(iteracion >= iteracionmax)
            condicion =1;
        end
        if (error_Total(iteracion) <= errormax)
            condicion =1;
        end
    end

    %Mostrar los Resultados
    set(handles.w11,'String',num2str(w11));
    set(handles.w12,'String',num2str(w12));
    set(handles.w21,'String',num2str(w21));
    set(handles.w22,'String',num2str(w22));
    set(handles.v1,'String',num2str(v1));
    set(handles.v2,'String',num2str(v2));
    set(handles.u21,'String',num2str(u21));
    set(handles.u22,'String',num2str(u22));
    set(handles.u3,'String',num2str(u3));

    %Dibujar el error
    axes(handles.axes1);
    x=0:1:iteracionmax;
    plot(x,error_Total,'color','r', 'LineWidth', 2);
end

function f = funcion_activ(z)
    %SIGNOIDE
    f = 1/(1+exp(-z));
end

function fp = derivada_fun_act(z)
    %SIGNOIDE
    fp = (1-funcion_activ(z))*funcion_activ(z);
end

ML V: Regularización y Regresión Lineal Bayesiana

Regularización
En el artículo anterior obtuvimos la función de regresión entre dos variables, que es un modelo matemático para el conjunto de datos dados, sin embargo se puede encontrar parámetros muy grandes por lo que es necesario agregar un factor de regularización llegando a obtener el siguiente problema:

Cuya solución al aplicar el gradiente para minimizar el error es:

Ahora debemos encontrar el parámetro lambda adecuado, pero antes observemos como afecta la variación de este parámetro:

Ahora con el uso de probabilidades encontraremos cual es el lambda adecuado, en la siguiente gráfica se observa como y en x1 esta efectado por ruido gaussiano, tal que la probabilidad de que se mida el dato t en es punto es:

Que se lee como: probabilidad de que sea t dado x,w y sigma (desviación estándar)  es igual a una distribucion normal de la variable t con media en y(x,w), que es la función de regresión, y varianza igual a sigma al cuadrado

Recordando el planteamiento del problema de regresión donde teníamos de datos los puntos dados (x1,t1), (x2,t2), ..., (xN,tN). Asumiendo que las probabilidades en cada punto son independientes se tiene:

Ahora aplicaremos logaritmos para pasar de las multiplicaciones a una sumatoria

Ahora asumamos una distribución gaussiana prior, o anterior , con distinta varianza y media 0, y podemos obtener una probabilidad posterior, la cual debemos maximizar.

Usando Bayes tenemos:

Donde el denominador por ser una integral con respecto a w, termina por no depender de w. Por eso maximizamos solo el numerador. Para pasar de la multiplicación a una suma volvemos a usar el logaritmo obteniendo al final:

Que es similar a la primera ecuación de este artículo, por tanto para obtener la Estimación Máxima a Posteriori (MAP ) debemos hacer lambda igual a la división de las varianzas.

Regresión Lineal Bayesiana
Usando MAP podemos encontrar ya parámetros adecuado pero que pasa si los datos son secuenciales, debemos buscar la manera de encontrar la probabilidad de un nuevo punto dados los puntos antiguos, a esto se llama la distribución predictiva:

   Esto se debe aplicar recursivamente tantas veces como nuevos puntos aparezcan.
Veamos un ejemplo, supongamos que tenemos y=-0.3+0.5x, e inicialmente varianza1=0.4 y varianza2=0.5.
Al principio sin ningún punto observado se tiene a priori:

El espacio de Hough se obtiene de una transformada que permite conocer si existe lineas rectas en el espacio de datos.

Al conocer el primer dato se tiene:

Al conocer el segundo dato:

Y así se va acercando cada vez mas a medida que se toman más datos, así con 20 datos:

Obtenemos la distribución predictiva integrando sobre todos los posibles parámetros del modelo:

La probabilidad a posterior puede encontrarse:

Donde Prior cov: Covarianza de la probabilidad a priori y Prior mean: media de la probabilidad a priori.
Podemos realizar un programa pero es mejor observar los resultados gráficamente:

Al igual que en el ejemplo anterior al agregar mas datos el modelo se vuelve más cercano al esperado.

Si bien una imagen vale más que mil palabras, a veces es más esclarecedor un ejemplo con palabras:

Imaginen que les presentan una foto, antes de verla les han dicho que lo que hay en  la foto es un animal.

Una vez que la ven, observan que tiene cuatro patas, es peludo y posee cola.

Luego les presenta otra foto de un animal de la misma especie, misma raza, ahora relacionan la características del animal de la foto anterior con las del animal de la nueva foto, por ejemplo el pelaje es café y los ojos y nariz son negros en ambos pero el uno es más pequeño y posee pelaje más corto.

Luego les presenta unas foto de un animal de la misma especie, pero diferente raza, si bien ahora hay más diferencias las semejanzas siguen siendo más numerosas, como orejas largas y hocico un tanto alargado.

Luego de muchas fotos más pueden reconocer un perro, no sabíamos que era un perro al inicio, sin problema de otra foto de un animal de otra especie.

Es lo que hemos estado realizando con la regresión bayesiana, con cada nuevo dato tenemos un modelo más reducido y por tanto reconocemos o clasificamos mejor nuevos datos que obtengamos. 

Además y para terminar:
Un modelo que se ha encontrado con el uso de regresión puede ser evaluado de diferentes maneras.
Esto se puede utilizar para ajustar los parámetros del modelo como el uso de un conjunto de datos de validación
La Regresión Lineal Bayesiana opera en datos secuenciales y proporciona la distribución predictiva.
Cuando se utiliza priores gaussianos (y ruido gaussiano), todos los cálculos se pueden hacer analíticamente, como todas las probabilidades siguen siendo gaussianas